Táčky u geometrie

Výsledky:

1. K tomu, aby zalil první záhonek, musí zahradník ujít 
             14 + 16 + 2,5 + 16 + 2,5 + 14 = 65m.
   Při zalévání druhého záhonu ujde
             14 + 2,5 + 16 + 2,5 + 16 + 2,5 + 2,5 + 14 = 65 + 5 = 70m 
   

   Při zalévání každého dalšího záhonku je potřeba ujít o 5 m víc než při zalévání předcházejícího záhonku.

   Máme tudíž aritmetickou posloupnost
             65, 70, 75, 80, 85, 90, 95, ..., 65 + 5 * 29.
   Součet členů této posloupnosti je
             [(65 + 65 + 29 * 5) * 30]/2 = 4125 m 
   Zahradník při zalévání celé zahrady ujde 4,125 km.
   

   ---

2. Na 1 cm² Zemského povrchu působí tlak 1,033 at, proto síla působící na povrch Země je přibližně 5,274*10¹⁸kp, neboť při poloměru 6378 km je zemský povrch zhruba 5,107*10¹⁸ cm². Vyřešte též v soustavě SI.

   ---

3. Ze vzorců pro obsah trojúhelníku lze sestavit rovnice av_a = bv_b = cv_c. Z nich pak plyne, že je a : b : c = 1/v_a : 1/v_b : 1/v_c anebo v_a : v_b : v_c = 1/a : 1/b : 1/c.
   Sestrojíme z daných výšek trojúhelník a z jeho výšek nový trojúhelník, podobný hledanému trojúhelníku, jehož konstrukce je již snadná

   ---

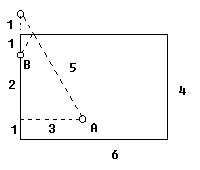
4. Průsečík H je ve výšce
             v = xy / (x + y) = 3*5 / (3 + 5) = 15/8 = 1,875 m . 
   

   ---

5. Délku drátu zjistíme na rozvinutém plášti. Je to přepona trojúhelníku s odvěsnami 3 m a 4 m dlouhá 5m.
   

   ---

6. a) Je to možné, neboť obdélník ABCD má dva vrcholy lichého stupně. Jsou to A, C b) Pravidelný šestiúhelník nesplňuje Eulerovu podmínku, neboť všechny jeho vrcholy jsou lichého stupně. Pokud by obsahoval právě dva takové vrcholy, byla by úloha řešitelná. Musela by však znít tak, že je třeba narýsovat pravidelný šestiúhelník a jednu úhlopříčku.

   ---

7. Z bodu A vedeme (přikládáním pravítka) přímku, která by byla co nejblíže k bodu B. Potom vedeme na ni z bodu B kolmici pomocí kružítka a bodem A vedeme stejně dlouhou kolmou úsečku. Tak dostaneme obdélník, v němž je hledaná spojnice úhlopříčkou. Delší strany rozpůlíme pomocí kružítka a získané body spojíme. Středem takto získané spojnice musí procházet úhlopříčka. Kdyby pravítko nestačilo, rozdělíme první přímku na vhodný počet dílů a v nich sestrojíme kolmice úměrné základnám, takže vlastně sestrojíme řadu stejnolehlých trojúhelníků, jejichž přepony tvoří hledanou přímku.

   ---

8. 
   

   ---

9. Tato úloha se zdá velmi složitá, je však vcelku jednoduchá, protože každý čtverec můžeme rozdělit na libovolný počet shodných obdélníků; tedy i v našem případě ho rozdělíme na 6 obdelníků.